Kelly Generalization

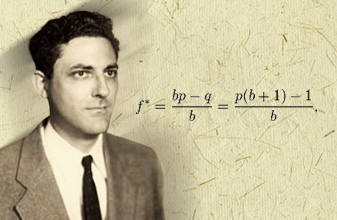
In this presentation I will show you how to apply Kelly betting to all factors which affect your betting. Up to now Kelly betting has been difficult to apply in today's casino environment. Negative expectation bets, minimum and maximum limits, cover strategy, tips, and expenses are not covered in current Kelly teachings, yet they affect your expected winnings and must be taken into consideration when sizing your bets for optimal growth.

For example, let's look at a Kelly bettor playing at a six deck shoe on the Strip. Say he has a $10,000 bankroll , counts using High-Low, and is betting a minimum of $15 and a maximum of $150. Between his minimum and maximum bets, he's betting the Kelly bet for each true count. His bets are $15 for true counts 0 or less, $31 at t.c. 1, $70 at t.c. 2, $110 at t.c. 3, $148 at t.c. 4, and $150 at t.c. 5 and above. Since he didn't consider his non-optimal bets at his minimum and maximum bets, effectively he would be betting at 29% above his optimal Kelly bets (1.29K) - I'll show you why later. If he adds any cover betting to his play, he may be overbetting even more. If you wish to bet optimally and maximize your expected rate of bankroll growth, you must consider all of your bets in the game.

Fixed Betting Strategy

I will first cover a fixed betting strategy, which may include negative expectation bets, cover strategy, minimum and maximum bets, and non-proportional bets. Any fixed betting strategy in which an advantage and standard deviation can be calculated for the game will be covered. What I mean by a "fixed" betting strategy, is one where the relative size of the bets stays the same, but the bets as a group can be scaled up or down depending on the size of your bankroll.

The betting strategy must specify the number of units to be bet at each true count or running count (for unbalanced counts). Cover strategy can also be included (e.g. only raise your bets after a win).

For this analysis we will define our bets in terms of our betting strategy (number of units at each betting decision) and our betting unit. Your betting unit is usually the smallest bet you make. If you are spreading from 1 to 4 in black chips, then your betting unit is one black chip or $100. If you are betting one red chip per true count, your betting unit is one red chip or $5. The betting unit depends upon how you define your betting strategy. The betting strategy for the 1 to 4 spread in black chips could be described as bets of 1 unit, 2 units, 3 units, and 4 units with the betting unit being one black chip or $100. Alternatively the betting strategy could be described as bets of 100 units, 200 units, 300 units, and 400 units with the betting unit being one dollar. For this analysis, the number of units in the betting strategy doesn't matter, only the relative size.

The betting unit is the key to sizing our bets. We will just increase or decrease the size of our betting unit depending upon the size of our bankroll and the advantage/variance of the game we're playing, keeping the betting strategy "fixed." Also we will define the advantage and variance of the game in terms of our betting unit. By defining the advantage and variance of the game in terms of the betting unit and not in terms of the average bet, each bet will be weighed equally and the Kelly analysis will be the same as for determining the optimal bet at each true count. The optimal bet calculation will also be the same.

Given that the unit bet is a fraction,(f ) of our bankroll, (B), and our unit bet is (f)(B), then the optimal size of our unit bet is when:

f = (advantage of game)/(variance of game)

Since the advantage is defined relative to our betting unit, it is simply the expectation in units for the game. It will be equal to the traditional "average advantage" multiplied by the "average bet." If you are using a simulation program, the best way to calculate the advantage of the game is: advantage = (total units won)/(number of initial hands) The advantage will depend upon the scale of the betting strategy. If the number of units in the betting strategy is doubled, i.e. from 1-4 to 2-8, the advantage will be doubled. Since the advantage depends upon the scale of the betting strategy, it does not describe the return of the game by itself. What does and is the best measure to compare any two games is: advantage/standard deviation. Doubling the scale of the betting strategy will have no effect on adv./s.d.

Using the 6 deck game above with the same betting strategy (1 unit = $1) as an example of how to calculate the optimal bets in a game: advantage=.2235 s.d.= 53.7, variance=2884.6, bankroll=$10,000 f=.2235/2884.6=.0000775, unit bet=fB=$.775 bets of 15, 31,70,110,148,150 units become $12,$24,$54,$85,$115,$116 bets when multiplied by the unit bet and rounded off . The ratio of the unit bet of the Kelly bettor who only considered the bets between his bet spread and the unit bet of this optimal calculation is: $1/$.775= 1.29 which is the number that I gave above.

Tips affect your bankroll and should also be considered. If you model tipping as just giving away a certain fraction of your advantage, then you can just reduce your advantage likewise in your optimal unit calculation. Some blackjack simulators support tipping. If you use one of them, just include the tipping and the advantage will automatically be adjusted.

Optimal Betting Strategy

To maximize the expected growth rate our bankroll, we also need to optimize our betting strategy. If we are flat betting, then our advantage will be less than zero for the shoe game. The betting strategy for the shoe game given above is good, but it can be better. The previous analysis of a fixed betting strategy leads us to the solution for optimizing any betting strategy with a fixed bet spread. Given the optimal betting fraction, f=adv./var,. for the fixed betting strategy, the average growth rate of one's bankroll for that game is: [(adv./s.d.)^2]/2 (s.d.= standard deviation). By maximizing the average or expected growth rate, the Kelly Criterion is satisfied. If you have done a simulation of the game in question with flat bets, the adv. and s.d. can quickly be recalculated for different betting strategies with a spreadsheet. Some simulators will do it for you. By trial and error you can adjust the bets so that adv./s.d. reaches its maximum (and thereby maximizing the expected growth rate). There are several properties which make the process easier. For counts between the minimum and maximum bets, the optimal betting units at each count will be proportional to the adv./var. of the count. You can just choose the minimum and maximum bets, keeping them the same throughout the trial and error process. The relative sizes are all that matter, whether a 1-10 spread is from 10-100 or 12-120 doesn't matter much except for some minor round off error. When the optimal betting strategy is determined, the optimal bets will actually turn out to be the regular Kelly bets of adv/var at each true count for bets between the minimum and maximum bets.

Here is an optimal betting strategy for the game above: 6 deck, DAS, S17, 75% penetration, High-Low count,10-100 spread: 10 at a true count of 0 or below, 32 at t.c. 1, 70 at t.c. 2, and 100 at t.c 3 or above with a resultant adv.=.18427, s.d=43.06, var.=1845.55, adv./s.d.=.4279%

The optimal betting strategy for this game ramps up quickly. If you were to leave when the count hit -1, the adv./var. for the game would increase and your optimal betting strategy would ramp up slower. However if you add some cover plays, the adv./var. would decrease and your optimal betting strategy would ramp up even faster.

Expenses

If you are taking money out of your bankroll, you also need to factor that into your optimal bet calculations. Expenses are similar to tips in that they reduce your apparent advantage. I'll define expenses as taking out a fixed amount every day out of your bankroll. Since expenses reduce your advantage, you must reduce your optimal bet size, but when you reduce your bet size the fixed expenses become a larger part of your advantage and you'll have to further reduce your bet size. The process will settle on a value if your expenses are ¼ or less of your expected winnings. A little algebra will solve the problem. If your expenses are a fraction, c, of expected earnings (with optimal betting), then your new optimal unit bet will be a fraction, d, of the original optimal unit bet, where d=[1+(1-4c)^(1/2)]/2 As you can see, if (c ) is greater than ¼ , then d is imaginary-in other words it will be impossible to bet optimally, you'd always be overbetting. When you take expenses out, the total of your expected winnings and your expenses will be a fraction, d , of the original expected earnings. You can calculate the expected win of a game with optimal play by: expected win = (advantage of game)(unit bet)(n)(B)=(adv)(adv/var)(n)(B) =(n)(B)(adv./s.d)^2 where n=number of hands played, B=bankroll, and var=s.d.^2

Appendix

Here are the basic equations supporting my application of Kelly. I assumed that the bets in blackjack are independent or stochastic.

Kelly (Generalized)

Lemmas: lnx^r=rlnx ; ln(1+x)= x - (x^2)/2 approximately for x near zero using the first two terms of the Taylor Series expansion

Given the equation for bankroll growth of an idealized blackjack game - only winning or losing your original bet:

Bn=[(1+f)^W][(1-f)^L]Bi

Bi= initial bankroll , Bn= bankroll after N bets , f= fraction of bankroll bet, N= number of bets, W= number of wins, L= number of loses, W'= win rate= average W/N, L'= loss rate= average L/N, a= advantage=W'-L', W'+L'=1, W'=(1+a)/2, L'=(1-a)/2

Average log growth of bankroll =Average [ln(Bn/Bi)]/N =Average [ln[(1+f)^W][(1-f)^L]]/N = Average [(W/N)ln(1+f) + (L/N)ln(1-f)] = W'ln(1+f) + L'ln(1-f) = [(1+a)/2][f-(f^2)/2] + [(1-a)/2][-f-(f^2)/2] = af-(f^2)/2

The maximum log growth of bankroll occurs at f=a (the familiar equation). This was for an idealized game with unit payoffs so the variance wasn't taken into account and f was near zero for the log expression.

If one spreads from 1 to m units, betting f,2f,3f....mf :

a(i)= advantage at i units bet ; x(i)= fraction of bets at i units ; S(i):= summation of i from 1 to m

Average log growth of bankroll=

S(i): ln[(1+if)^[[1+a(i)]x(i)/2]] [(1-if)^[[1-a(i)]x(i)/2]] = S(i): ia(i)x(i)f - (i^2)x(i)[f^2]/2

maximum occurs at dS(i)/df = 0 , where f=[S(i): ia(i)x(i)]/[ S(i): (i^2)x(i)] = advantage/variance

The advantage and variance are relative to the unit bet. While I used an idealized model for blackjack payoffs, this can be modified by using final payoffs instead of initial bets and the results are the same. Therefore the variance should be the variance of the payoffs.